Keccak-256算法详解
keccak-256
keccak-256是以太坊采用的哈希加密函数,其与标准的SHA3-256仅仅在padding方式上有所不同,但是产生的结果是完全不一样的,我们主要关注以太坊使用的keccak-256。
keccak函数族采用了海绵结构,可以接受任意长度的输入,也可以提供任意长度的输出。keccak函数有两个用以描述其加密难度的参数:
- r:bitrate,表示加密时每一轮输入的数据比特数,决定了数据输入的长度
- c:capacity,表示加密时数据的额外比特数,与参数r共同决定了哈希操作的数据长度
b=r+c
keccak函数工作可以分为输入和输出两个主要的阶段,每个阶段都依赖于海绵结构,海绵结构中具有b比特的数据。(要求\(b=25*2^{l}\),其中\(l \in [0, 6]\))
在哈希函数工作前,首先按照比特率r对数据进行padding对齐,实现的方法为在数据后添加最少数量的10*1,使数据的长度为r的倍数,记得到的新数据\(P =
M||pad[r]\)。(标准的SHA3-256唯一不同的地方在于其修改了padding的方式,这导致了哈希结果巨大的差异)
在输入阶段,海绵结构在初始状态下是全0的b比特数据。依次向“海绵”中输入r比特的待加密数据,与海绵结构的前r比特进行异或,再通过加密函数f()得到新的海绵结构。不断重复上述过程直至对齐后的待加密数据全部输入海绵结构。
在输出过程中,依次从“海绵”中取出前r比特数据作为输出,如果长度小于要求的输出长度,则再通过加密函数f()得到新的海绵结构,重复取出前r比特数据直至长度大于等于要求。取得到的数据的前n位作为输出,即是keccak-n算法的哈希结果。
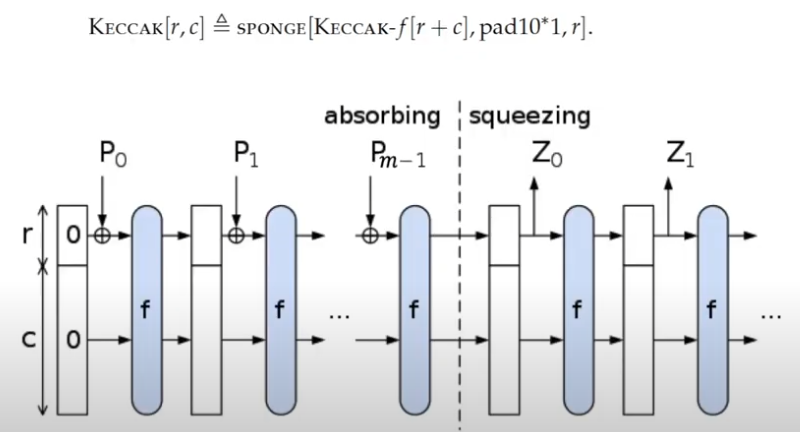
接下来的重点是加密函数f(),这是keccak函数族更新海绵结构的核心,f()函数以b比特数据作为输入,以b比特数据作为输出。将b比特的数据排列为一个三维矩阵,将其中的一个元素记为a[x][y][z],\(x, y \in [0, 5), z \in
2^{l}\),特别地当b=1600时,可以将a[x][y]视为一个5x5的64位整型数组。f()函数会执行n_{r}=12+2l轮加密,每一轮加密由五个部分组成,接下来按照顺序依次介绍这五个部分。
需要补充的是以下的运算都定义在GF(2)上,加法即为异或操作,乘法即为与操作。
\(\theta: a[x][y][z] = a[x][y][z] + \sum_{y'=0}^{4} a[x-1][y'][z] + \sum_{y'=0}^{4}a[x+1][y'][z-1]\)。直观地理解\(\theta\)操作,将矩阵a的每一行与上一行,下一行进行异或操作,其中下一行需要进行循环左移一位。
\(\rho: a[x][y][z] =
a[x][y][z-(t+1)(t+2)/2]\),其中\(t \in
[0, 24)\)并且在GF(5)域中满足\(\begin{pmatrix} 0 & 1 \\ 2 & 3
\end{pmatrix}^{t} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix}
x \\ y \end{pmatrix}\),特殊地当\(x=y=0\)时,令\(t=-1\)。\(\rho\)操作只对每个整形内部的比特顺序进行调整。
\(\pi: a[x][y] = a[x'][y'], \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 2 & 3\end{pmatrix} \begin{pmatrix} x' \\ y'\end{pmatrix}\)。 \(\pi\)操作只改变整形间的顺序。
\(\chi: a[x] = a[x] + (a[x+1] + 1)a[x+2]\)。\(\chi\)操作对行间进行操作,对数据进行杂凑加密。
\(\iota: a = a + RC[i_{r}]\)。\(\iota\)操作异或上轮常数进行混淆,其中轮常数只有64位,因此值改变了a[0][0]的值。
在实际实现中,可以通过预先计算好的常数对\(\rho, \pi\)操作优化加速。